这篇笔记包括lecture15、16,继续介绍关系的相关内容。
相容关系和覆盖
集合的覆盖(cover)指将集合分为非空的子集,每个元素至少属于一个子集。划分一定是覆盖,但覆盖不一定是划分。对于集合 A A A C C C
∅ ∉ C \varnothing \notin C ∅ ∈ / C ( ∀ x ) ( x ∈ C → x ⊆ A ) (\forall x)(x \in C \rightarrow x \subseteq A) ( ∀ x ) ( x ∈ C → x ⊆ A ) ∩ C = A \cap C = A ∩ C = A
覆盖的定义只是去除了划分的最后一条要求(子集不相交)。类似地,覆盖也可以定义关系 R = { < a , b > ∣ ( ∃ C 0 ) ( C 0 ∈ C ∧ a ∈ C 0 ∧ b ∈ C 0 ) } R = \{<a,b>|(\exist C_0)(C_0 \in C \land a \in C_0 \land b \in C_0)\} R = { < a , b > ∣ ( ∃ C 0 ) ( C 0 ∈ C ∧ a ∈ C 0 ∧ b ∈ C 0 )}
相容关系
相容关系(compatible relation)指具有自反性和对称性的关系。对于集合 A A A R R R C ⊆ A ∧ C = { x ∣ ( x ∈ A ) ∧ ( ∀ y ) ( ( y ∈ C ) → x R y ) } C \subseteq A \land C = \{x|(x \in A) \land (\forall y)((y \in C) \rightarrow xRy)\} C ⊆ A ∧ C = { x ∣ ( x ∈ A ) ∧ ( ∀ y ) (( y ∈ C ) → x R y )} C C C C C C C C C C R C_R C R
对于 A A A C C C C R C_R C R C ⊆ C R C \subseteq C_R C ⊆ C R C 0 ⊆ C 1 ⊆ . . . ⊆ C R C_0 \subseteq C_1 \subseteq ...\subseteq C_R C 0 ⊆ C 1 ⊆ ... ⊆ C R
C 0 = C C_0 = C C 0 = C C i + 1 = C i ∪ a j C_{i + 1} = C_i \cup {a_j} C i + 1 = C i ∪ a j j j j a j ∉ C j ∧ ( x ∈ C i → a j R x ) a_j \notin C_j \land (x \in C_i \rightarrow a_jRx) a j ∈ / C j ∧ ( x ∈ C i → a j R x )
对于 A A A R R R A A A C R ( A ) C_R(A) C R ( A )
偏序关系
偏序关系和拟序关系
如果 ( ∀ a ) ( ∀ b ) ( ( a ∈ A ∧ b ∈ A ∧ a R b ∧ b R a ) → a = b ) (\forall a)(\forall b)((a \in A \land b \in A \land aRb \land bRa) \rightarrow a = b) ( ∀ a ) ( ∀ b ) (( a ∈ A ∧ b ∈ A ∧ a R b ∧ b R a ) → a = b ) A A A R R R
自反的、反对称的、传递的关系是偏序关系(partial-order relation)。有偏序关系 R R R A A A < A , R > <A,R> < A , R >
如果 ( ∀ a ) ( a ∈ A → a R a ) (\forall a)(a \in A \rightarrow a\cancel{R}a) ( ∀ a ) ( a ∈ A → a R a ) R R R
非自反的、传递的关系称作拟序关系(quasi-order relation或strict order relation)。拟序关系是反对称的。
对于拟序关系 R R R R ∪ R 0 R \cup R_0 R ∪ R 0 R R R R − R 0 R - R_0 R − R 0
哈斯图
对于拟序集,以 < A , ≤ > <A, \le> < A , ≤> x , y ∈ A , x ≠ y , x ≤ y x, y \in A,x \not = y,x \le y x , y ∈ A , x = y , x ≤ y z z z x ≤ z ∧ z ≤ y x \le z \land z \le y x ≤ z ∧ z ≤ y y y y x x x A A A R = { < x , y > ∣ x ∈ A ∧ y ∈ A ∧ ( y c o v e r s x ) } R = \{<x,y>|x \in A \land y \in A \land (y covers x)\} R = { < x , y > ∣ x ∈ A ∧ y ∈ A ∧ ( yco v ers x )} A A A c o v ( A ) cov(A) co v ( A )
将 A A A < a , b > <a,b> < a , b > a a a b b b
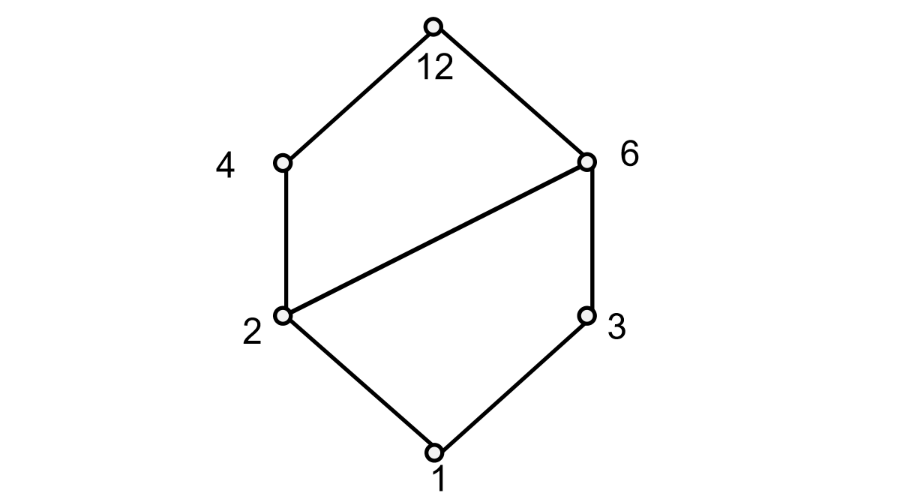
例如,下面是 A = { 1 , 2 , 3 , 4 , 6 , 12 } A = \{1,2,3,4,6,12\} A = { 1 , 2 , 3 , 4 , 6 , 12 }
利用拟序关系和偏序关系的性质,可以将它们的关系图简化为哈斯图。
上确界和下确界
对于偏序集 < A , ≤ > <A,\le> < A , ≤> B ⊆ A B \subseteq A B ⊆ A y ∈ B y \in B y ∈ B ( ∀ x ∈ B ) ( x ≤ y ) (\forall x \in B)(x \le y) ( ∀ x ∈ B ) ( x ≤ y ) y y y B B B y ∈ B y \in B y ∈ B y ≤ x y \le x y ≤ x x = y x = y x = y y y y B B B x ∈ B ∧ ( ∀ y ) ( y ∈ B → x ≤ y ) x \in B \land (\forall y)(y \in B \rightarrow x \le y) x ∈ B ∧ ( ∀ y ) ( y ∈ B → x ≤ y ) x x x B B B x ∈ B ∧ ( ∀ y ) ( ( y ∈ B ∧ y ≤ x ) → x = y ) x \in B \land (\forall y)((y \in B \land y \le x) \rightarrow x = y) x ∈ B ∧ ( ∀ y ) (( y ∈ B ∧ y ≤ x ) → x = y ) x x x B B B
对于偏序集 < A , ≤ > <A,\le> < A , ≤> B ⊆ A B \subseteq A B ⊆ A y ∈ A ∧ ( ∀ x ) ( x ∈ B → x ≤ y ) y \in A \land (\forall x)(x \in B \rightarrow x \le y) y ∈ A ∧ ( ∀ x ) ( x ∈ B → x ≤ y ) y y y B B B C C C C C C B B B x ∈ A ∧ ( ∀ y ) ( y ∈ B → x ≤ y ) x \in A \land (\forall y)(y \in B \rightarrow x \le y) x ∈ A ∧ ( ∀ y ) ( y ∈ B → x ≤ y ) x x x B B B C C C B B B
上界和下界不一定存在,也可能不止一个。上确界和下确界要么不存在,要么只有一个。
全序关系和链
在偏序集 < A , ≤ > <A, \le> < A , ≤> x ∈ A x \in A x ∈ A y ∈ A y \in A y ∈ A x ≤ y x \le y x ≤ y y ≤ x y \le x y ≤ x x x x y y y x x x y y y x x x y y y ≤ \le ≤ A A A < A , ≤ > <A, \le> < A , ≤> A A A
如果 B B B x x x y y y B B B A A A ∣ B ∣ |B| ∣ B ∣ x x x y y y B B B A A A ∣ B ∣ |B| ∣ B ∣
偏序集可以被分成不相交的反链。如果链的最大长度为 n n n n n n n n n n n n < A , ≤ > <A, \le> < A , ≤> A A A m n + 1 mn + 1 mn + 1 A A A m + 1 m + 1 m + 1 n + 1 n + 1 n + 1
良序关系
对于偏序集 < A , ≤ > <A, \le> < A , ≤> A A A ≤ \le ≤ < A , ≤ > <A, \le> < A , ≤>
良序集是全序集。有限全序集是良序集。
闭包的定义
对于非空集合 A A A R R R R ′ R^{'} R ′ R ′ R^{'} R ′ R ′ R^{'} R ′ R R R A A A R ′ ′ R^{''} R ′′ R ⊆ R ′ ′ → R ′ ⊆ R ′ ′ R \subseteq R^{''} \rightarrow R^{'} \subseteq R^{''} R ⊆ R ′′ → R ′ ⊆ R ′′ R ′ R^{'} R ′ R R R r ( R ) r(R) r ( R ) s ( R ) s(R) s ( R ) t ( R ) t(R) t ( R )
对于关系 R R R R 是自反的 ⇔ r ( R ) = R R是自反的 \Leftrightarrow r(R) = R R 是自反的 ⇔ r ( R ) = R R 是对称的 ⇔ s ( R ) = R R是对称的 \Leftrightarrow s(R) = R R 是对称的 ⇔ s ( R ) = R R 是传递的 ⇔ t ( R ) R是传递的 \Leftrightarrow t(R) R 是传递的 ⇔ t ( R )
闭包的构造与性质
对于非空集合 A A A R R R r ( R ) = R ∪ R 0 r(R) = R \cup R_0 r ( R ) = R ∪ R 0 s ( R ) = R ∪ R − 1 s(R) = R \cup R_{-1} s ( R ) = R ∪ R − 1 ∣ A ∣ = n |A| = n ∣ A ∣ = n t ( R ) = R ∪ R 1 ∪ . . . ∪ R n t(R) = R \cup R_1 \cup ... \cup R_n t ( R ) = R ∪ R 1 ∪ ... ∪ R n
< a , b > ∈ R n <a, b> \in R^n < a , b >∈ R n n n n a a a b b b R R R R + = R ∪ R 2 ∪ . . . R^+ = R \cup R^2 \cup ... R + = R ∪ R 2 ∪ ... R n R^n R n R + = R 1 ∪ R 2 ∪ . . . ∪ R n R^+ = R^1 \cup R^2 \cup ... \cup R^n R + = R 1 ∪ R 2 ∪ ... ∪ R n
可以用warshall算法来计算传递闭包。
如果 R R R s ( R ) s(R) s ( R ) t ( R ) t(R) t ( R ) R R R r ( R ) r(R) r ( R ) t ( R ) t(R) t ( R ) R R R r ( R ) r(R) r ( R ) s ( R ) s(R) s ( R )
r s ( R ) rs(R) rs ( R ) r ( s ( R ) ) r(s(R)) r ( s ( R )) r s ( R ) = s r ( R ) rs(R) = sr(R) rs ( R ) = sr ( R ) r t ( R ) = t r ( R ) rt(R) = tr(R) r t ( R ) = t r ( R ) s t ( R ) ⊆ t s ( R ) st(R) \subseteq ts(R) s t ( R ) ⊆ t s ( R )